Physics
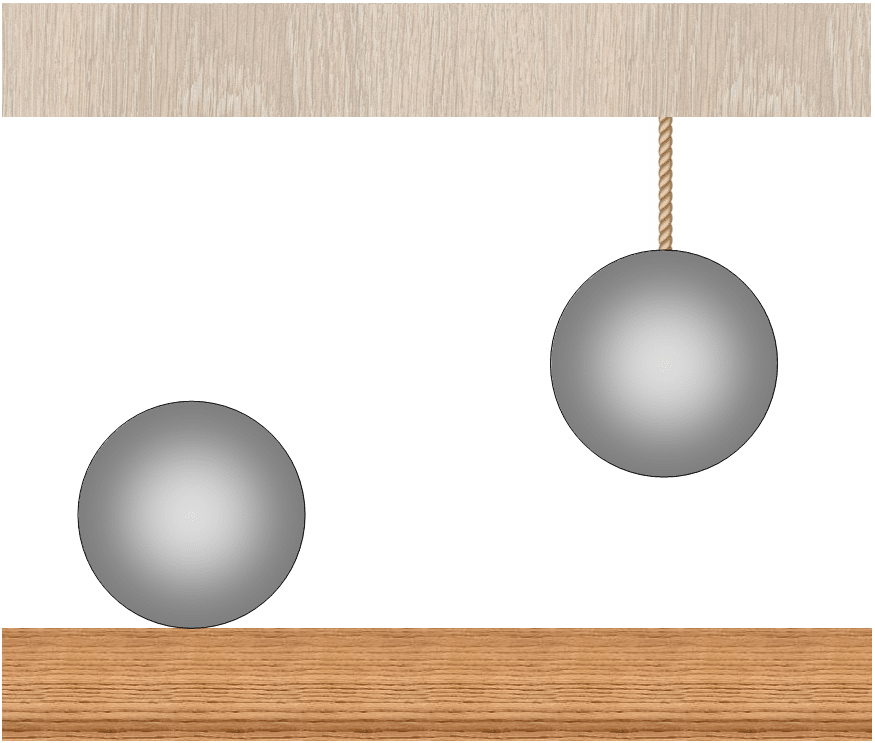
“There are two identical balls that are at the same temperature. One of them lies on a horizontal surface, the other is suspended on a string. Both balls are given the same amount of heat in physics. Will the balls be the same after this? (Any kind of heat loss can be neglected.) “
This problem can sometimes be found at the Olympiads in physics or in social networks. The conventional answer is intuitively clear: because of the energy expended on thermal expansion in the presence of gravity, the ball lying on the horizontal surface will be colder than the hanging on the filament. In a recent article it was shown that this answer is incorrect. In fact, the result will be reversed: the lying ball will be warmer than the hanging ball. We will understand why the traditional method of solving this problem leads to an incorrect answer, and why intuition in this case brings us down.
The traditional solution is based on the following chain of reasoning. Both balls will expand as they heat up, because of this, the center of mass will rise slightly at the ball lying on the horizontal surface, and the center of mass near the hanging ball will drop. As a result, the reclining ball will heat up more weakly, since some of the heat transferred to it will be expended to raise it, and the hanging ball will heat up more by additional work of gravity when it is lowered.
The reasoning used in the traditional solution: due to thermal expansion, the ball lying on the table rises, and the ball hanging on the thread drops.
The answer can be expressed by a simple formula for the temperature difference of the underlying (19459013)
) and the hanging one (
) balls:
where
and
– mass, radius and heat capacity of the balls,
– acceleration of gravity,
– the coefficient of the line Of the thermal expansion of the material of the balls, which we consider to be sufficiently small. As can be seen,
<img src = ” alt = ” $ T_1 <t_2$” data-tex=”inline”></t_2$”> <t_2$” data-tex=”inline”></t_2$”> [imgsrc=” https://habrastorage.org/getpro/geektimes/post_images/95e/e56/921/95ee569211f80af44f02d2fa041b9e41.svg “- the lying ball will be colder.
It would seem that everything is logical in this decision. “The first swallow,” demonstrating that there is something wrong here is a mental attempt to create a heat engine on the basis of a ball.
The machine can work as follows: first the ball lies on the table where we heat it, For which its center of mass rises. Then we fix the ball on the hanging thread from above and gently remove the table, so that the ball’s height does not change. Finally, we cool the ball to its original temperature, as a result, the ball shrinks and its center of mass rises. Result: part of the heat that we transmitted to the ball when it was heated, turned into a mechanical work on its rise, and this cycle can be repeated endlessly.
Cycle The operation of a heat machine based on a ball: after heating and cooling the ball has risen, which means that we have turned some of the heat into a mechanical work.
The problem here is that by increasing the ball radius, the efficiency (Efficiency) of such a machine can be made arbitrarily close to 100%. This contradicts the second law of thermodynamics, according to which the efficiency of a heat engine can not exceed the efficiency of the Carnot cycle at the same temperatures of the heater and refrigerator.
Why is the traditional solution of the problem wrong? Here it is necessary to take into account that the ball lying on the table from the very beginning, until its heating, will be slightly flattened by the force of gravity, and the hanging ball will be slightly stretched. This will negatively affect the efficiency of the above described thermal machine: during the suspension, the ball will drop slightly, because of this, the efficiency will decrease and will no longer exceed the efficiency of the Carnot cycle.
The influence of gravity on balls: the ball lying on the table is flattened, and the hanging on the thread is stretched.
How will this manifest itself in the consideration of the original problem? It turns out that the compression or stretching of the material changes its heat capacity: in the case of a compressed material, heating at the same temperature will require less heat than in the case of a stretched material. Consequently:
- When the ball lying on the table is heated, some of the heat will go to its rise due to thermal expansion; But, together with this, the heating of the material of the ball will be easier and will require less heat.
- When a ball hanging on a string is heated, the work of gravity, when lowered, will be added to the heat transferred to it; But, at the same time, the heating of the ball material itself will be more laborious and will require more warmth.
The traditional solution takes into account only the factors indicated by white arrows. Ignoring the factors shown by the black arrows leads to an erroneous answer.
As we see, in both cases there are factors that work both in favor of one variant of the answer (the lying ball can turn out to be colder than the hanging one), and in The opposite side (the lying ball can be warmer than the hanging one).
It would seem that the effect of a change in the heat capacity of a material when it is compressed or stretched, even if it exists, should be very small, and it can be neglected, as it is done in the traditional solution of the problem. However, it is not. This effect is of the same order of smallness as the thermal expansion itself, since both of these effects result from the anharmonicity of the interatomic forces. Taking into account one of these effects in the traditional solution, in combination with ignoring the other, is inconsistent and leads to an erroneous answer.
The article shows that if the problem is solved correctly, the difference in the temperature of the balls after transferring the same amount of heat to them is
where
– absolute temperature of the balls,
– the rate of change in the coefficient of thermal expansion of the material of the balls with a change in its temperature.
Compared to the result of the traditional solution, the temperature difference is:
- The opposite sign, since for most materials the value of
is positive, so the entire right side of the equation is also positive, and
.
- Much smaller in absolute value, because here, instead of a small value, even smaller values appear
<img src = ” https://habrastorage.org/getpro/geektimes/post_images/b86/a5a/a2d/ B86a5aa2d08343576f332107a3ab9544.svg ” alt = ” $ alpha ^ 2 $ ” data-tex = ” inline ” />and.
Thus, the two effects discussed above completely compensate each other, but the second of them (the change in heat capacity during compression or stretching) is slightly stronger than the first (thermal expansion).
The authors of the article conduct a rather rigorous analysis of the problem, but, unfortunately, they do not give a clear explanation of how exactly almost complete compensation of the two effects takes place, so it was necessary to understand this in this matter.
The figure shows a typical dependence of the potential energy of interaction of atoms on the distance Between them. The force acting on the atoms is directed toward the decrease of the potential energy, therefore the atoms strongly repel each other at short distances and are weakly attracted at large distances. At some distance
<img src = ” https://habrastorage.org/getpro/geektimes/post_images/684/06a/ae6/68406aae60d6e93c48a4ffb52616739f.svg ” alt = ” $ r_0 $ ” Data-tex = ” inline ” />the potential energy reaches a minimum. The desire of atoms to this most energetically favorable distance is the reason for their binding into molecules, liquids and solids.
Now we will figure out where the thermal expansion of materials comes from. With chaotic thermal motion, the distance between atoms is no longer equal strictly
<img src = ” https://habrastorage.org/getpro/geektimes/post_images/684/06a/ae6/68406aae60d6e93c48a4ffb52616739f.svg ” alt = ” $ r_0 $ ” data-tex = ” inline ” />but fluctuates near this value. The bond between atoms has the property of anharmonicity: it behaves like an asymmetric spring, which is easier to stretch than to squeeze. As a consequence, with thermal motion, the bond is stretched most of the time, but not compressed, so the average distance
<img src = ” https://habrastorage.org/getpro/geektimes/post_images/a36/64e/814/a3664e8141bb9e32f63fee08f47dfd45 .svg ” alt = ” $ langle r rangle $ ” data-tex = ” inline ” />between atoms becomes larger than
<img src = ” data-tex = ” inline ” ” [info] [info] />. With increasing temperature, this effect increases, the distances between atoms increase and the material expands.
Cause of thermal expansion of materials: with thermal motion, the average distance between atoms increases Due to the anharmonicity of the forces of interatomic interaction.
What happens when the material is compressed or stretched, as in the case of flattened or stretched balls? When the material is compressed, the external force decreases the average distance between atoms, and increases when the tension is increased.
During compression, the equilibrium distance between atoms decreases, .
Now we are ready to understand how the compression and stretching of the material affects its heat capacity. Imagine that we squeezed the material, so that the distance between atoms during thermal motion is now oscillating near the equilibrium position shifted to the left. Anharmonicity does not disappear anywhere, therefore, as before, when heated, the average distance between atoms will increase. But at the same time we will shift back to the minimum of potential energy, which means that the energy of the material will be further reduced! This explains the decrease in the heat capacity of the material during compression: thermal expansion leads to a small additional decrease in the energy of interatomic interactions, therefore less material is required for material heating.
If the material is stretched, then the situation Inverse: with thermal expansion, the energy of interaction of atoms will grow faster than in unstretched material. Therefore, to heat the stretched material at the same temperature, it takes a little more energy than without stretching, and therefore the heat capacity of the stretched material will be higher.
So, on the example of the Olympiad problem, which for many decades has been solved (and, perhaps, Continue to solve) erroneously, we see that real physics sometimes contradicts our intuition. Therefore, it is so important in solving problems to use the mathematical apparatus accurately, without being limited to superficial reasoning.
Based on the article materials:
Giacomo De Palma, Mattia C. Sormani, Counterintuitive effect of gravity on the heat capacity of a solid sphere: Re-examination of a well-known problem, American Journal of Physics 83, 723 (2015).
Publicly available article preprint: arxiv.org/pdf/1502.01337








